外角は内角の補角である (内角) (外角) =180° (外角) =180°− (内角)解:根據三角形內角和=180°,可以列出下列式子: 85°33°∠C=180° ∠C=180°−85°−33°=62° ∠C∠1 =180° ∠C外角=∠1=180°−62°=118°動画一覧や問題のプリントアウトはこちらをご利用ください。ホームページ → http//19chtv/ Twitter→ https//twittercom/haichi_toaru
多角形とは 外角 内角の和 面積 対角線の本数の公式と求め方 受験辞典
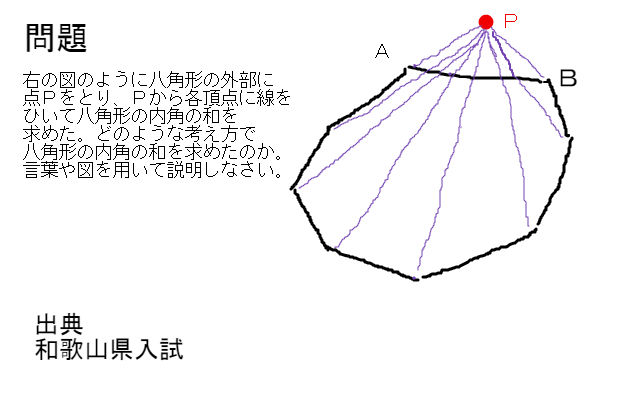
八角形の外角の和
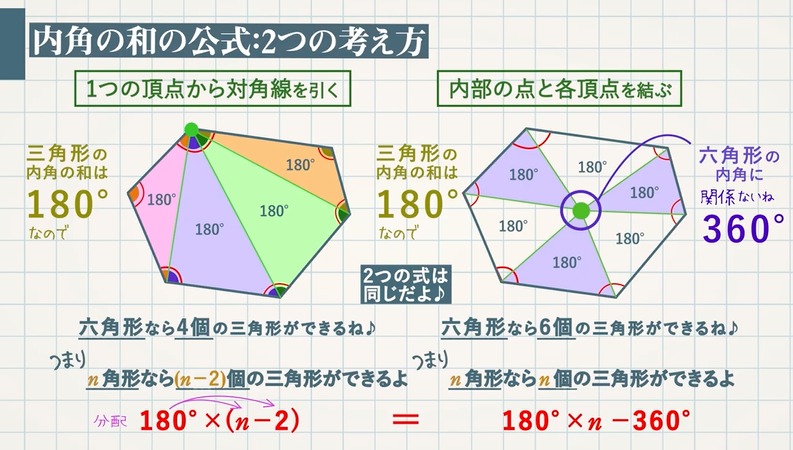
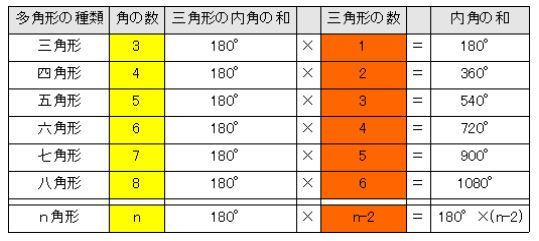
八角形の外角の和-N個の内角とn個の外角の総和は, 180°×n (1) 外角の和は 360° (2) したがって, 内角の和は (1)−(2) 180°×n−360°=180°×(n−2) 図5 (証明 2) 1つの三角形の内角の和は 180° 図6で示されるように, n角形は n−2 個の三角形に分けられるから,内角の和は (n−2)×180°八角形の内角の和は1080度である。 項目を8本の放射線に分けて、8つの項目の大小を対比する図表を、「オクタゴンチャート 要曖昧さ回避 」という。;




正多角形の内角と外角の大きさ 具体例で学ぶ数学
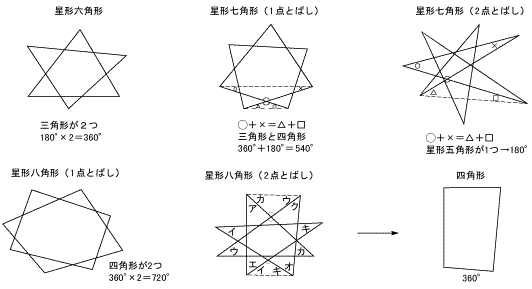
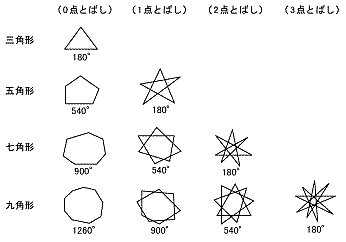
頂点とする三角形の角の和から五角形の外角の 和を2つ分ひき,180°と求めることができる。 B ①では,図形の性質を利用することで星型五角形 の内角の和を演繹的に求める例をあげた。では, 結ぶ点の数を増やしたときに内角の和はどうな るだろうか。多角形の角の 大きさの和に ついて、三角形 の内角の和が 180°であるこ とをもとに理 解している。 (エ) 7 単元の学習内容を活用し、八角形 の内角の和を様々な方法で求める ことができる。 ・ 八角形の内角の和が1080°であ ることを様々な考え方で説明す る。課題学習の指導(数学) 1. 教材 「星形多角形の内角の和を追究しよう」(2年) 2. 教材観 三角形や多角形の内角の和を学習した後で,発展問題としてよく扱われる教材である。 星形五角形だけとっても,その形のきれいさで生徒の興味・関心を
(3) 十八角形の外角の和を求めなさい gc_十角形の外角の和htm gc_六角形の外角の和htm gc_三平方の定理半円塗り潰しhtm gc_三平方の定理半円でhtm gc_三平方の定理半円でhtm gc_三平方の定理正三角形でht 多角形の外角の和は、どんな多角形でも必ず360度になります 已知多これも星形正五角形と同じ方法でやれます。 奇数の星形は、このように証明すればいいのです。 証明 先の尖った三角形が9個あります。だから、 180度×9=16度 中にある七角形の外角の和が2つ分あります。 360度×2=7度4 星形 n 角形の角の和 星形七角形を,内側の七角形の各辺を延長してできた図形と考える。 内側の七角形のまわりにできた7つの三角形の内角の和の合計は, 180°×7=1260° また,七角形hijklmnの外角の和は360°だから,
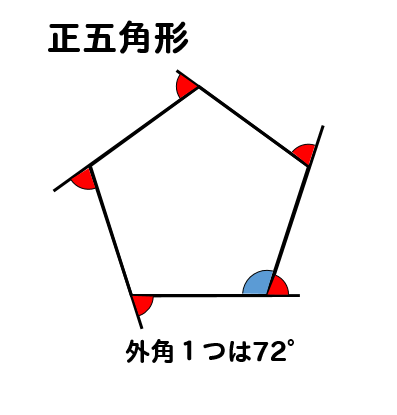
(3) 正五角形では5つの外角の和は ゜だから1つの外角は ゜ したがって1つの内角は ゜です. 何角形でも外角の和は360° この問題は五角形の内角の和が540°になることを使っても求められるが,初めの2つの空欄を埋めるには,問題文で指定された順に答える方がよい.平行と合同 例題 平行線の錯角・同位角 補助線を引く問題 三角形の内角と外角の関係 印をつけた角の和 角の二等分線と内角の和 三角形の合同証明1 三角形の合同証明2(辺の共通) 三角形の合同証明3(角の180°×2=360° となった。 五角形の場合も同じように考えると、 3 つの三角形がで きるので、内角の和は 180°×3=540° 六角形の内角の和は、 180°×4=7° n 角形の場合を考えると、一つの頂点から対角線を引い てできる三角形の数は



正多角形の1つの内角 外角を求める方法を問題解説 数スタ




小学校5年 算数 正多角形の角の大きさ Youtube
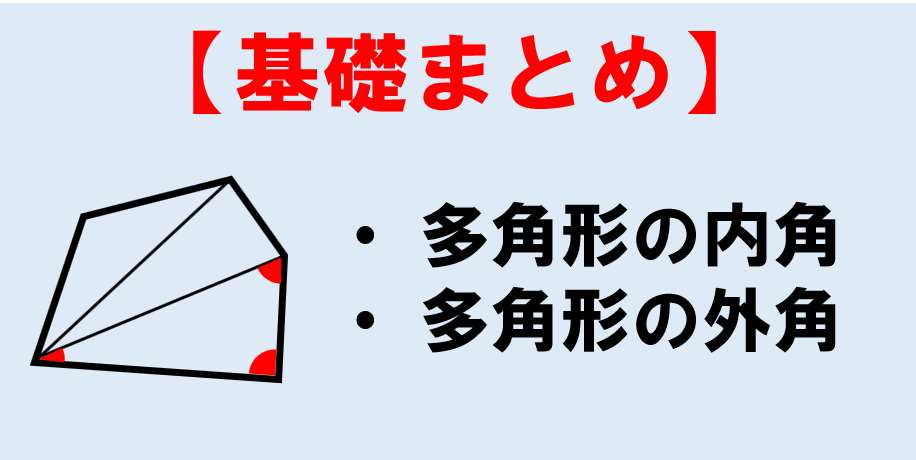
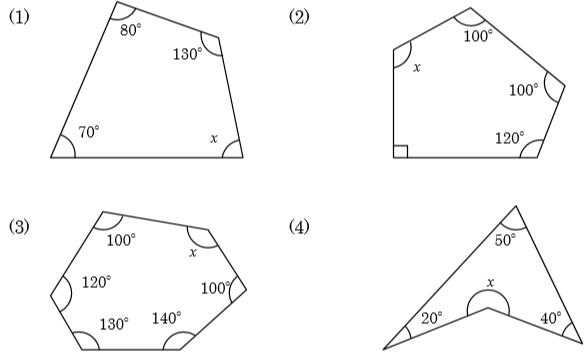
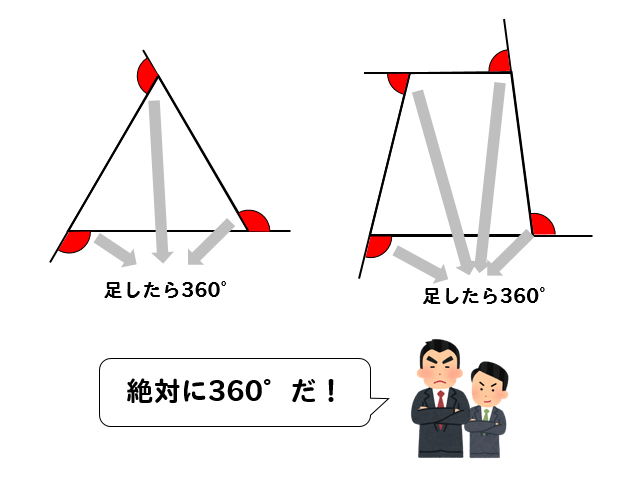
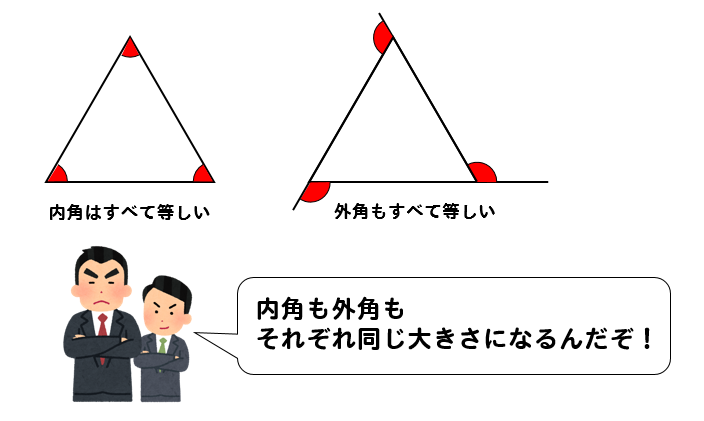
図形の性質の調べ方 平行線と角(3) 1 次の図で、l mのとき、∠x、∠yの大きさを求めなさい。同じ印をつけた角は それぞれ等しい。 (1) (2) (3) 243 x 70° 115° E x l 40° m x l ° m x l 10° m正多角形の内角・外角 まとめ お疲れ様でした! 外角の和は常に360°になる という性質は非常に便利でしたね。 問題でも大活躍する性質なので 絶対に覚えておきましょう。 内角が問題に出てきた場合でも $$\large{(内角)(外角)=180°}$$ (三角形の内角の和) = 180° (四角形の内角の和) = 360° ここまでは大抵の人が知っていると思いますが、六角形や八角形などを覚えている人は少ないかもしれません。 そこで今日は 簡単に覚えられる多角形の内角の和を紹介していこうと思います。



多角形の外角の和 On Vimeo



多角形とは 外角 内角の和 面積 対角線の本数の公式と求め方 受験辞典
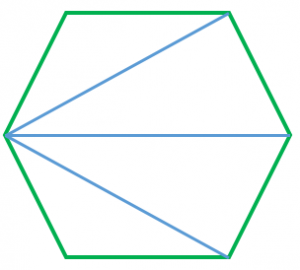
三角形が6個もふくまれている八角形の内角の和は、 180°を6倍して「1080°」になるってことさ。 まとめ:八角形には三角形が6個もかくれている! 八角形の内角の和をもとめたいときは、 180°(n2) という公式のnに「8」をいれちゃえばOK。 計算すると1080 3分でわかる!多角形の外角の和の求め方 多角形の外角の和ってどうなるの?? こんにちは!この記事をかいているKenだよ。弾丸旅行にはまっているね。 多角形(n角形)の内角の和は、 180°×(n2) で計算できたね。 ここで、好奇心旺盛なヤツはこう思うはずだ。五边形内角和 和一个内角是多少度 六边形七边形八边形九边形十 90;



2




3分でわかる 多角形の外角の和の求め方 Qikeru 学びを楽しくわかりやすく
内角の和・外角の和の証明 なぜn角形の内角の和が180°×(n2)となり、外角の和は360°になるのか見ていきましょう。 内角の和について 多角形の内角の和は小学校のときに習ったと思うので復習にな八邊形 ,或者叫 八角形 ,係有8條直邊嘅 多邊形 ,總共有8隻角,內角和1080°。 睇 傾 改 多邊形 1 10 一角形 二角形 三角形 四邊形 五邊形 六邊形 七邊形 八邊形 九邊形 十邊形 11 十一邊形 十二邊形 十三邊形 十四邊形 十外角=外角と隣り合わない内角の和 例えば下図の三角形の外角=3050=80度です。 上式を覚えておけば簡単に外角が算定できます。 なぜ外角=外角と隣り合わない内角の和となるか解説します。 三角形の内角の和は180度です。 角度の大きさをA、B、Cと
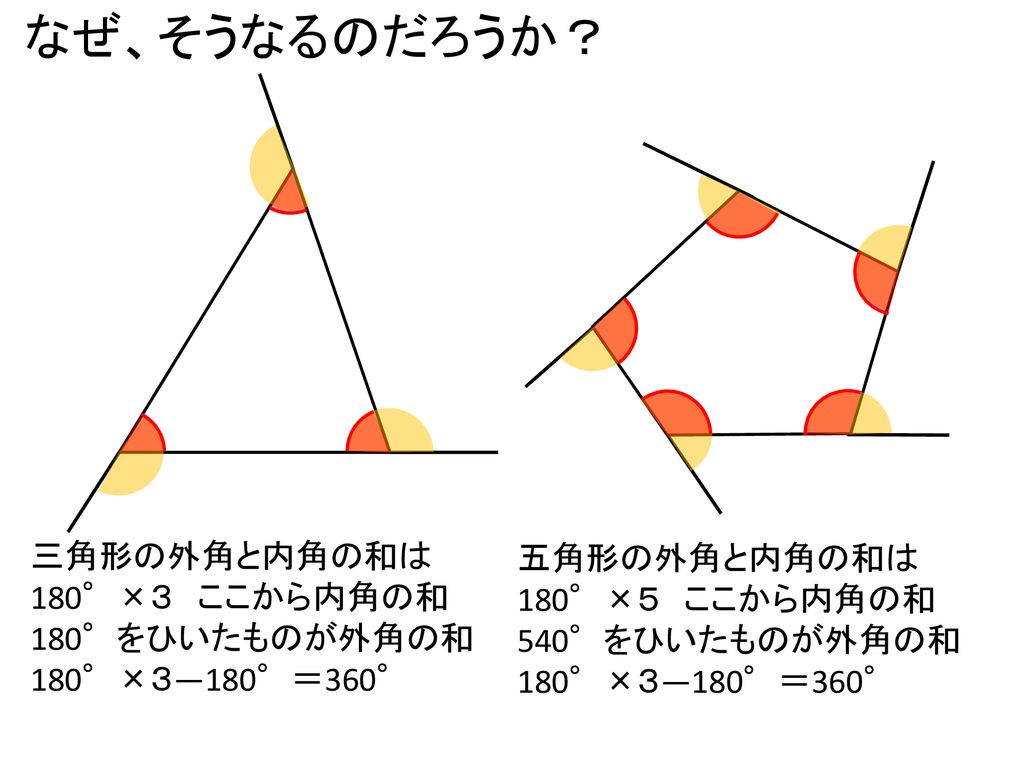



多角形の外角の和 凹型四角形の角 星形五角形の内角の和 Ppt Download
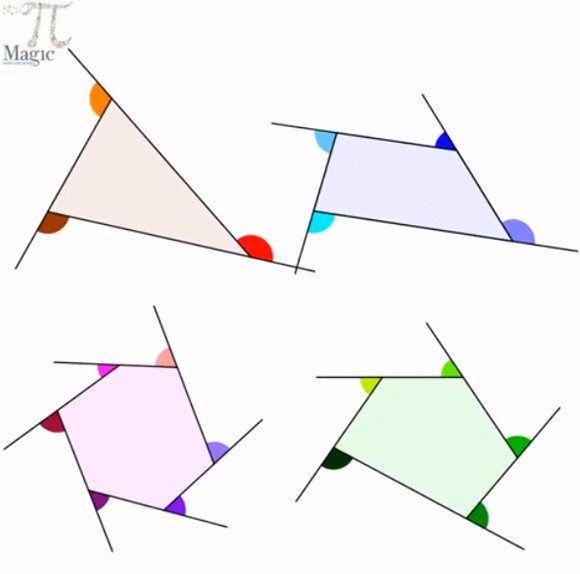



多角形の外角の和は360度 をgifアニメで表現 これがわかりやすいと海外で話題に カラパイア
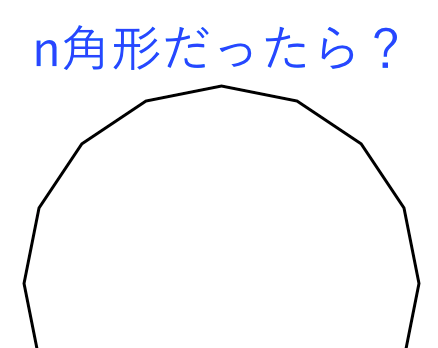
つまり、 n の値に関係なく,外角の和は 360° になる。 出典 フリー百科事典『ウィキペディア(Wikipedia)』 ( 59 UTC 版) 多角形の内角の和/外角の和 n 角形の内角の総和は、多角形の形状に関わらず(凸であれ凹であれ) である。 これはどのような多角形でも、対角線で適当に区切ることで (n2) 個の三角形に分割できることから導かれる。四角形と同じように、三角形の数が分かれば内角の和は求められますよね^^ どうですか?ここまではそれほど難しくないと思います。 多角形と言っても、まだまだ五角形、六角形と数が少ない形ですからね。 ということで!




多角形の内角の和 外角の和の公式 数学fun



18年10月29日の記事 時空先生のドリルプリント
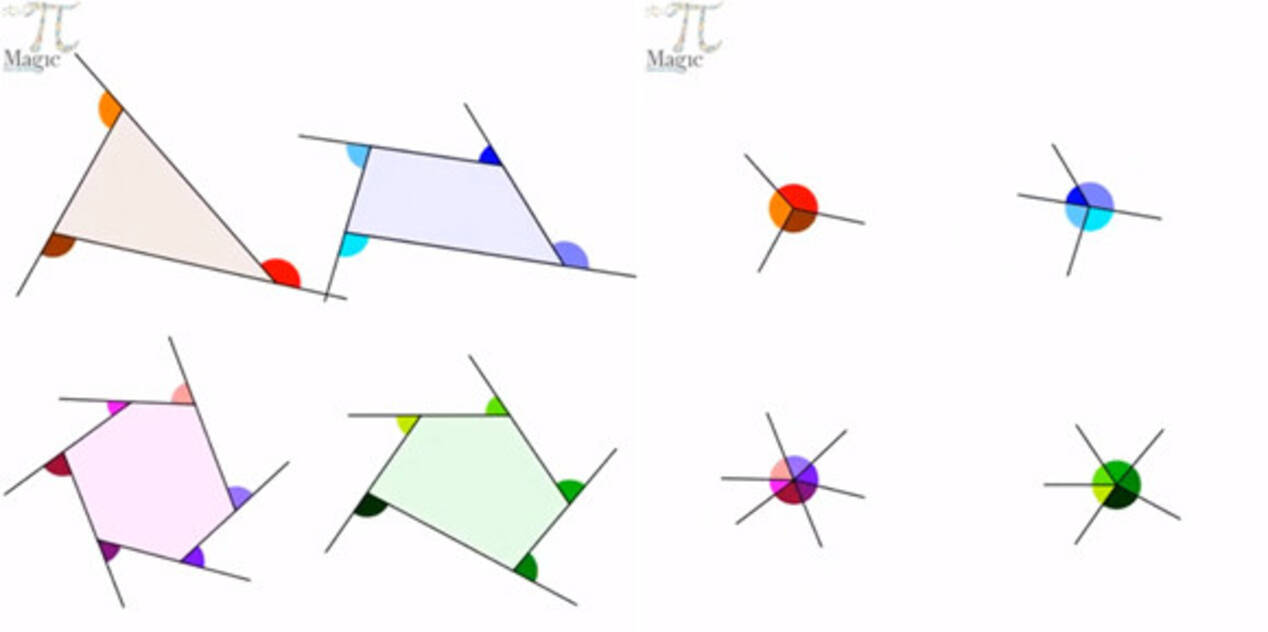
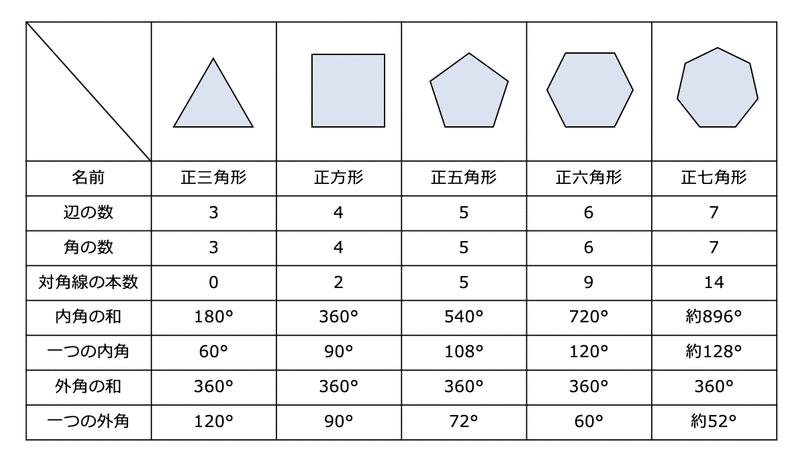
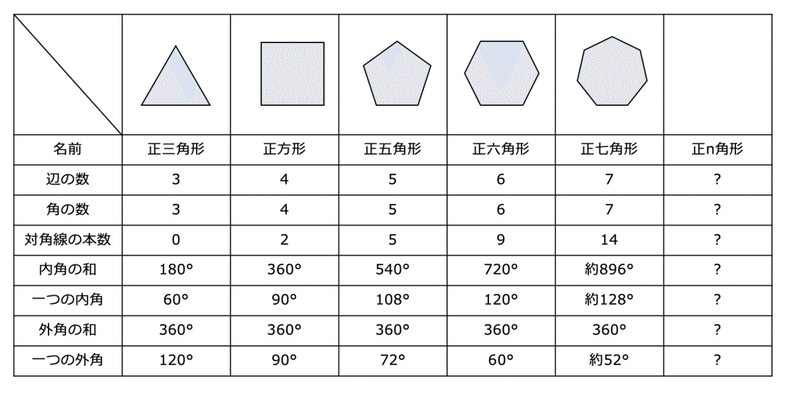
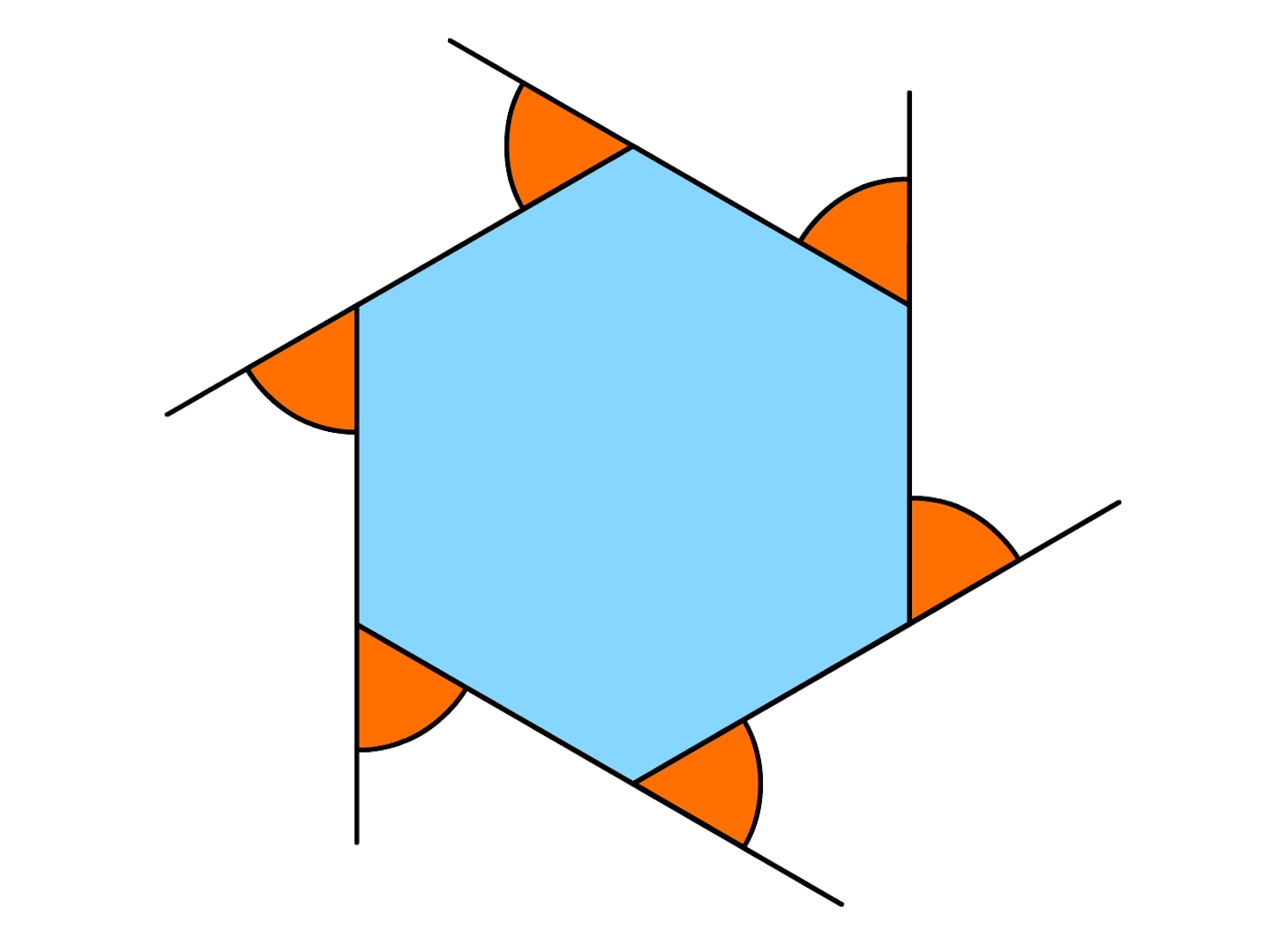
2年 多角形の外角|数学イメージ動画集|大日本図書 五角形の外角を全部合わせると 360° です。 同様に,他の多角形でも外角の和は 360° になります。 このことから,多角形の外角の和はいつも 360° になるということがわかります。 実施時期 2年生2多角形の角の大きさの和について考えましょう。 (3)多角形の辺の数と,角の大きさの和を表にまとめましょう。 (4)表を使って,八角形,九角形の角の大きさの和を求めましょう。 八角形: 九角形: 三角形 四角形 五角形 六角形 七角形 外角・内角の和、面積、対角線の本数の公式と求め方 21年2月19日 この記事では、「多角形」の種々の公式(外角の和・内角の和、面積、対角線の本数など)やその求め方をわかりやすく解説していきます。 また計算問題の解き方もわかりやすく解説して




数学 中2 51 多角形の内角と外角の和 基本編 Youtube




多角形の外角の求め方を5分でサクッと理解 中学数学 理科の学習まとめサイト
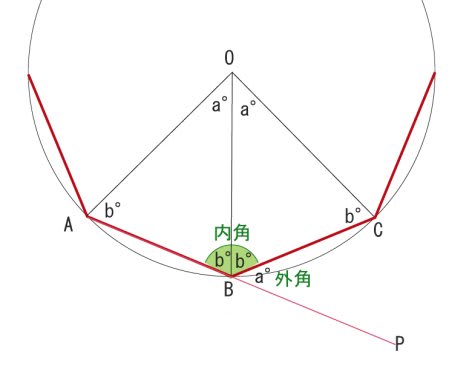
多角形の外角の和 内容 n角形の外角の和は、360°である。 証明 三角形の場合 三角形の一つの外角は他の2つの内角に等しいので、外角の和は、内角の和を2回足したことになるので三角形の外角金属环形垫片是用金属材料加工成截面形状为八角形或椭圆形的实体金属垫片,具有径向自紧密封作用。 金属环形垫片是靠垫片与法兰梯形槽的内外侧面 (主要是外侧面)接触,并通过压紧而形成密封的。 金属环垫分为八角环形垫和椭圆垫两种。 金属环形垫片 为什么任意多边形的外角和为360度? (中学) 证明方法:① N边形有N条边,那么延长N条边的一端,就会有N个180°。 ② 每一个180°都由内角外角构成。 ③ N边形内角和(用划分三角形个数计算)为 (N2)180°④ N边形的外角和为N180° (N2)180°=360°




課題学習の指導 数学




4章 平行と合同 2 多角形の外角の和 Ppt Download




八角形 Wikipedia




中2数学 多角形の内角の和と外角の和のポイントと練習問題 Pikuu




正十八角形の1つの内角の大きさを求めなさい この問題の解き方教えてください Clear



Http Www Asahikawa Hkd Ed Jp Nagayama Jhs 221 Ef 92 E5 B9 B4 E6 95 B0 E5 Ad A6 Ef E5 9b E5 80 80 E5 9a E8 92 E5 81 Ae E5 86 85 E8 92 81 A8 E5 96 E8 92 80 80 E8 A3 E7 Ad 94 Ef Pdf
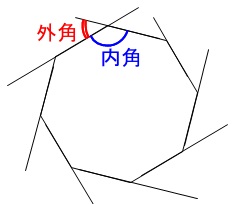



多角形の内角の和の公式と外角の和を利用した角度の求め方
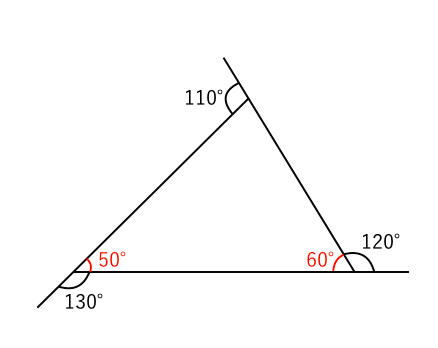



図形の調べ方 外角を求める 苦手な数学を簡単に



正八角形内の角度 渋谷教育学園渋谷中学 受験算数問題より どう解く 中学受験算数
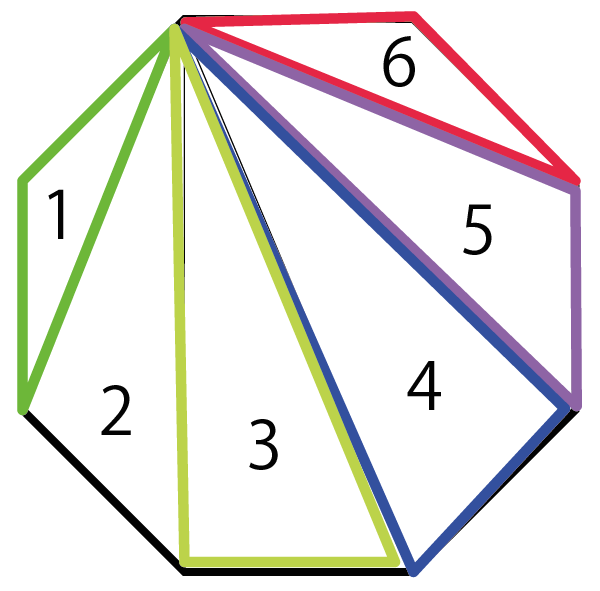



3分でゲット 八角形の内角の和がわかる公式 Qikeru 学びを楽しくわかりやすく
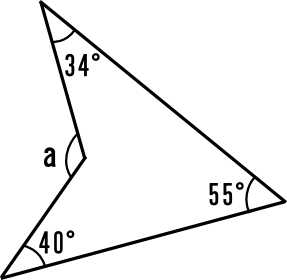



中学2年数学練習問題 図形の調べ方 多角形の内角と外角の解答




多角形の内角の和の公式と外角の和を利用した角度の求め方
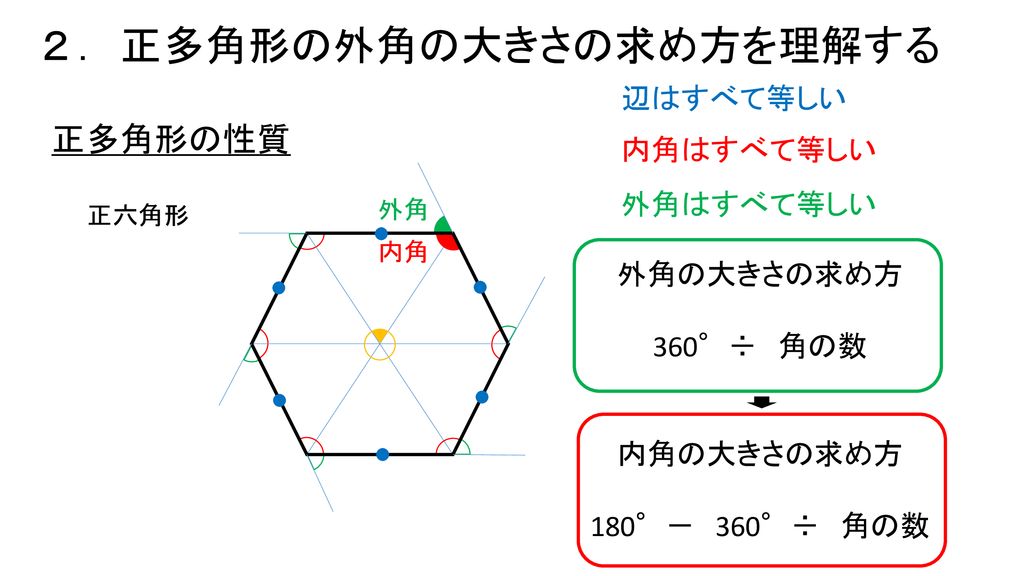



正多角形の作図 プログラミングで多角形を描く方法を考えよう 1時間目 Ppt Download



720度 星形九角形の角度の和




多角形の内角の和 外角の和は 正多角形の内角の求め方は 証明や問題をわかりやすく解説 遊ぶ数学




多角形の内角の和 外角の和は 正多角形の内角の求め方は 証明や問題をわかりやすく解説 遊ぶ数学



多角形とは 外角 内角の和 面積 対角線の本数の公式と求め方 受験辞典



内角の和 180 N 2 外角の和 360 教遊者




3分でゲット 八角形の内角の和がわかる公式 Qikeru 学びを楽しくわかりやすく



みんなの算数講座 第31講座 中学受験 家庭教師 東京の算数家庭教師さんじゅつまん




内角の和 と 外角の和 名寄 算数数学教室より




多角形の内角の和 外角の和の公式 数学fun



2



720度 星形九角形の角度の和



1



子供からの質問です 正八角形の一つの内角の大きさと 対角線の数を求めなさ Yahoo 知恵袋



720度 星形九角形の角度の和



多角形の外角の和は360度 をgifアニメで表現 これがわかりやすいと海外で話題に 19年5月22日 エキサイトニュース



Cmsweb2 Torikyo Ed Jp T Chu Kyou Shin Action Common Download Main Upload Id 112



課題学習の指導 数学



正多角形の1つの内角 外角を求める方法を問題解説 数スタ



中2数学 多角形の内角の和 外角の和まとめ 授業わかるーの Byナオドット先生 中学数学のわかりやすい解説サイト



Http Www Pref Osaka Lg Jp Attach 6629 Jmw 2b4 3 Pdf



図形の調べ方 N角形について 内角の和を求める 苦手な数学を簡単に




多角形の外角の求め方を5分でサクッと理解 中学数学 理科の学習まとめサイト



2



みんなの算数講座 第31講座 中学受験 家庭教師 東京の算数家庭教師さんじゅつまん



図形問題の徹底演習 八角形の内角の和 中学数学 理科 寺子屋塾の復習サイト



2



六角形的角度




図形問題の徹底演習 八角形の内角の和 中学数学 理科 寺子屋塾の復習サイト



内角攻め それとも外角攻め すうがくラボのブログ



実践例 プログラミングで正多角形を学ぶ 山崎智仁 Tomohito Yamazaki Note



内角 外角 180 どうして 名寄 算数数学教室より




多角形の内角の和 外角の和は 正多角形の内角の求め方は 証明や問題をわかりやすく解説 遊ぶ数学




無料 中2数学 基本解説 解答プリント 223 図形3 多角形の角



3




外角 多角形



Www City Hadano Kanagawa Jp Www Contents Simple C050a Pdf



Http Www Fukui City Ed Jp Meido J Pdf 2 3 2 4 Pdf



中2数学 多角形の内角の和と外角の和のポイントと練習問題 Pikuu




内角の和 180 N 2 外角の和 360 教遊者




正多角形の内角と外角の大きさ 具体例で学ぶ数学




多角形の内角の和 外角の和の公式 数学fun




多角形 四角形 五角形 六角形 の内角の和の公式 問題の解き方 数学fun



正多角形の1つの内角 外角を求める方法を問題解説 数スタ




多角形の内角の和 外角の和は 正多角形の内角の求め方は 証明や問題をわかりやすく解説 遊ぶ数学
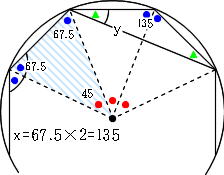



Mathematics 算数のコツ 1 角度の問題は 等しい角を見つけて書き込む 働きアリ




多角形の内角の和 外角の和は 正多角形の内角の求め方は 証明や問題をわかりやすく解説 遊ぶ数学




正多角形の 内角が あっという間に分かる術 名寄 算数数学教室より




1つの内角の大きさが 1つの外角の大きさの8倍である正多角形を答えなさい この問題の Clear



多角形の内角と外角 思考力を鍛える数学




無料 中2数学 基本解説 解答プリント 227 図形7 復習



正8角形です あ い う それぞれの角度の求め方を教えてください 一つの角の Yahoo 知恵袋




なんで かっこ1番nー2 15なんですか Clear



正多角形の1つの内角 外角を求める方法を問題解説 数スタ




多角形の内角の和 外角の和の公式 数学fun



Http Hokusuukyou Cyuu Com 17 2 Zukei Pdf




多角形の英語 五角形 六角形 八角形 12角形 正多角形など 英語独学マスター



1



Fzk Ed Shizuoka Ac Jp Shizuchu Wp Content Uploads Sites 4 17 02 5b4511dfa47fa1a398d0591ccee2 Pdf




数学の家庭教師 90分 サッカー個人 少人数レッスン Plus




3分でわかる 多角形の外角の和の求め方 Qikeru 学びを楽しくわかりやすく



正多角形の内角と外角の大きさ 具体例で学ぶ数学




内角の和 180 N 2 外角の和 360 教遊者




中2数学 正多角形の外角の大きさが3秒でわかる公式 Qikeru 学びを楽しくわかりやすく




なぜ内角の和は180 N 2 になるのか Youtube



正5角形の角度の求め方は 1分でわかる値 内角の和 正6角形 正8角形の角度は



Www Kyo Kai Co Jp Img Material Chuu 38s Kw S2 Mihon Pdf



課題学習の指導 数学



1




内角の和 180 N 2 外角の和 360 教遊者



Fzk Ed Shizuoka Ac Jp Shizuchu Wp Content Uploads Sites 4 17 02 5b4511dfa47fa1a398d0591ccee2 Pdf



南山中学女子部過去問題演習



2年 多角形の外角 数学イメージ動画集 大日本図書




3分でわかる 多角形の外角の和の求め方 Qikeru 学びを楽しくわかりやすく




十八角形 Wikipedia




内角の和 180 N 2 外角の和 360 教遊者




3分でゲット 八角形の内角の和がわかる公式 Qikeru 学びを楽しくわかりやすく




多角形の性質 第2回 多角形の内角の和の求め方 算数パラダイス




中学2年の数学 動画 多角形の内角と外角の和 計算編の問題 19ch




3分でわかる 多角形の外角の和の求め方 Qikeru 学びを楽しくわかりやすく



0 件のコメント:
コメントを投稿